Parser combinator notes

These are my notes from the lecture by Scott Wlaschin, available at YouTube.

Scott uses F# at his slices, though I am not using F# but Rust, so I will rewrite as well as my ability permits to Rust code.

Parsing is a crucial task in computer science, as it allows us to process and interpret data that goes into our programs. There are many approaches to parsing, and parser combinators are one powerful and flexible tool for building parsers.

Scott explains what parser combinators are and how they work. He starts by looking at the basics of simple parsers that can match individual characters or patterns in input data. From there, he expands on combinator functions to compose parsers into more complex ones. This essay will take a very close approach to Scott, building over his slides and my implementation with explanations about the code.

Parsing a single character

Let us start by creating a simple parser that matches the character 'A'.

First, we will need an enumerator for returning errors. The code is self-explanatory. Two edge cases cause failure; either we have an empty input string, or the character we are matching against ('A') is not present in the place we expect it to be within the input chars.

enum ParserError<'a> {
    EmptyInput,
    NotFound(&'a str),
}

Then we have a parser function, pcharA, which verifies if the first character matches with 'A' and returns the remaining slice from the original input if successful.

fn pcharA(input: &str) -> Result<&str, ParserError> {

	// We return an error if the string is empty.
	// It may be empty because the parser has finished
    if input.is_empty() {
        Err(ParserError::EmptyInput)
    }

	// If it is not empty, we match the first character of the string with 'A'
	else if input.chars().nth(0).expect("Found empty string") == 'A' {
		// If it is a match, we return an Ok status with the remaining string.
		// We do this because we can continue to parse from where this function
		// lefts it.
        Ok(&input[1..])
    }

	else {
		// If it's not a match, we return an error status.
        Err(ParserError::NotFound(input))
    }
}

As for now, we can visually see this function as a microchip with one input pin and two possible output pins, one for failure and another for an Ok status.

The next update is to make this code accept any character match_char to parse.

The update demands we update the error enumerator to include more information, what the character expects, and what it found.

#[derive(Debug)]
enum ParserError {
    EmptyInput,
    NotFound { expected: char, found: char },
}

The function is no longer named pcharA per the function's ability to parse any given char from any given string input.

fn pchar(input: &str, match_char: char) -> Result<(char, &str), ParserError> {
    if input.is_empty() {
        Err(ParserError::EmptyInput)
    }
	// The only difference is that it matches the input character
	else if input.chars().nth(0).expect("Unexpected empty str") == match_char {
        Ok((match_char, &input[1..]))
    } else {
		// In case of failure, we return more information as context.
        Err(ParserError::NotFound {
            expected: match_char,
            found: input.chars().nth(0).expect("Unexpected empty str"),
        })
    }
}

The updated microchip of our parser now looks like the following image.

We can then call the parser to test it out as follows:

fn main() {
    // Ok(('A', "BACADDA"))
    println!("{:?}", pchar("ABACADDA", 'A'));

    // Err(NotFound { expected: 'B', found: 'A' })
    println!("{:?}", pchar("ABACADDA", 'B'));

    // Err(EmptyInput)
    println!("{:?}", pchar("", 'A'));
}

We can take advantage of the Ok status return type since it contains a reference to the remaining input to parse to create parsing loops that end when the remaining is empty.

fn main() {
    let input = "ABABBBAAB";
    let mut remain = input;
    let mut match_char = 'A';

    loop {
        match pchar(remain, match_char) {
            Ok((matched, rem)) => {
                println!("Found {matched}, remaining: {rem}");
                remain = rem;
            }
            Err(ParserError::EmptyInput) => {
                println!("Remaining is empty");
                break;
            }
            Err(ParserError::NotFound { expected, found }) => {
                println!("Found {found} but expected {expected}");
                match_char = match match_char {
                    'A' => 'B',
                    'B' => 'A',
                    c => panic!("Found unexpected char {c}"),
                };
            }
        }
    }
}

The code above is an elementary example of a toy parser that looks for characters {'A', 'B'}. When an unexpected char is encountered, the matching char changes to the other alternative, if the character is not 'A' nor 'B' then a panic occurs. The point here is we can loop over the remaining string to parse until we find an Err(ParserError::EmptyInput), in which case we know the remaining string to parse is empty, and thus we have finished parsing.

Taking it to purely functional

Up to now, there is nothing strange about these two past functions, they are what we all expect them to be. Though, the next step turns up the thing to be more interesting.

Instead of having a function that takes a character to match while parsing, we are making a function that can craft functions. This is, instead of building a function to parse x char, we are programming a function that can build another function that parses a constant, bounded character.

To fully understand this, let us take a closer look at the concept of function-builder functions. A function-builder function is a function that creates and returns another function. It takes one or more arguments, and the function that gets returned is bound to those arguments.

Within Rust, as with many other languages, we have a concept named closure A closure is an anonymous function that we can bind to variables and pass as an argument to other functions. In the parser world, and thanks to functional programming languages, this allows us to make complex combinations of small closures to create complex parsing systems with ease.

With this in mind, pchar is now becoming a function-builder function that looks something like this:

Hence, pchar is a closure builder. The resulting closure looks:

Another way to see this new paradigm is to interpret pchar as a function factory that records in metal that the character the function is building will match.

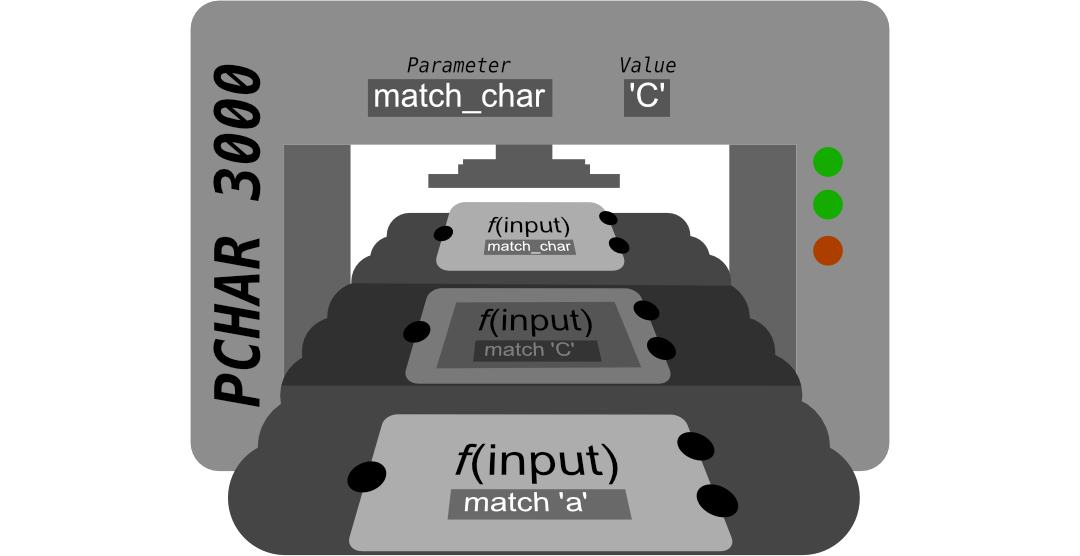
Note how match_char got embedded in the closure and thus is no longer required as one of the closure inputs, allowing us to wire together various parser functions to create more complex parsers, similar to wiring microchips together to build computers.

The pchar function-builder code is the following:

fn pchar(match_char: char) -> impl Fn(&str) -> Result<(char, &str), ParserError> {
    move |input| {
        if input.is_empty() {
            Err(ParserError::EmptyInput)
        } else if input.chars().nth(0).expect("Unexpected empty str") == match_char {
            Ok((match_char, &input[1..]))
        } else {
            Err(ParserError::NotFound {
                expected: match_char,
                found: input.chars().nth(0).expect("Unexpected empty str"),
            })
        }
    }
}

I rewrote the function to be more functional, continuing with the functional spirit of the paper, as follows:

fn pchar(match_char: char) -> impl Fn(&str) -> Result<(char, &str), ParserError> {
    move |input| {
        input
            .chars() // Get an iterator over the characters
            .next() // Step to the next char (the first one)
            .ok_or_else(|| ParserError::EmptyInput) // Yield error if empty
            .and_then(|ch| { // Else, perform an action with the char (ch)
                if ch == match_char {
                    Ok((match_char, &input[1..]))
                } else {
                    Err(ParserError::NotFound {
                        expected: match_char,
                        found: ch,
                    })
                }
            })
    }
}

Specific to Rust, look at the return type described in the signature.

fn pchar(..) -> impl Fn(&str) -> Result<(char, &str), ParserError>

The impl part means we are dealing with the Rust trait system. pchar returns a value that complies with being a function with an immutable state with a string slice (&str) as input and a Result with specific types for error and ok statuses as its output.

Within the function, we return a closure. This closure, as the signature implies, takes an input and returns Result<(char, &str), ParserError> from its code block:

move |input| { .. }

There are two steps to use the code; create a parser function and call it with an input to parse.

fn main() {
    println!("{:?}", pchar('A')("ABAABABA"));
}

Or written in a longer form:

fn main() {
	let parseA = pchar('A'); // Create a parse function
	let result = parseA("ABAABABA") // Use the function
    println!("{result:?}");
}

To end this first functional stage, we will create a trait "alias" for the trait impl Fn(&str) -> Result<(char, &str), ParserError> generic over T instead of char.

The resulting block of code with the new type is:

#[derive(Debug)]
enum ParserError { /* fields */ }

// We add the Parser trait alias
trait Parser<V>: Fn(&str) -> Result<(V, &str), ParserError> {}
impl<V, T: Fn(&str) -> Result<(V, &str), ParserError>> Parser<V> for T {}

// Now pchar returns a type that implements the trait Parser<char>
fn pchar(match_char: char) -> impl Parser<char> {
    move |input| { /* code */ }
}

fn main() {
    let parseA = pchar('A'); // Create a parse function
    let result = parseA("ABAABABA") // Use the function
    println!("{result:?}");
}

In the code listed above first we create a trait Parser that requires that types that want to implement it also implement the Fn(&str) -> Result<(V, &str), ParserError> trait.

Then, we create a blanket implementationi of Parser<V> for every type T that implements Fn(&str) -> Result<(V, &str), ParserError>.

In this step we implemented the Parser trait for all closures that follow the rule, thus achieving an alias for the closure signature.

Combining parsers

and_then

Execute one parser, if it succeeds execute a second one. If any fails, return the error.

fn and_then<V>(parser1: impl Parser<V>, parser2: impl Parser<V>) -> impl Parser<Vec<V>> {
    move |input| {
        let (res1, remain1) = parser1(input)?;
        let (res2, remain2) = parser2(remain1)?;
        Ok((vec![res1, res2], remain2))
    }
}

or_else

Try to execute one parser, if it fails, execute a second parser. If both fail return an error.

fn or_else<V>(parser1: impl Parser<V>, parser2: impl Parser<V>) -> impl Parser<Vec<V>> {
    move |input| {
        if let Ok((res, remain)) = parser1(input) {
            Ok((vec![res], remain))
        } else {
            let (res, remain) = parser2(input)?;
            Ok((vec![res], remain))
        }
    }
}

map

Apply a function transformation to the result of a parsing function.

fn map<V, K>(parser: impl Parser<V>, f: impl Fn((V, &str)) -> (K, &str)) -> impl Parser<K> {
    move |input| Ok(f(parser(input)?))
}